This is the story of my encounter with the FridgeIQ puzzle and the computer science rabbit-holes it dragged me into.
While the technical part is interesting I am most impressed by the fact, that someone has done it all without the aid of machines. Read on to find out more.
Chapter #0 – Meet The Game
Fridge IQ is a tangram-like disection-puzzle that comes in the form of 16 polygonal pieces cut from magnetic foil so they stick to objects like fridge doors – hence the clever name.

Each piece is labeled with a single letter. In the box there are equally magnetic challenge cards. On these cards you, the player, are asked to complete triangles, rectangles and squares from different subsets of the pieces:
While working through these challenges it quickly becomes obvious how the pieces have to be placed on an (invisible) grid – which is different from classic tangram. Thus the shape and size of the target shape can easily be derived from the available pieces and so these challenges are not that hard to solve.
Chapter #1 – Why Stop There?
The person I got this game from added the story of Gerald who, when faced with this game, took it a step further by generating a plethora of additional challenges which are also much much more interesting.
Geralds challenges each use all parts and they have beautiful fourfold mirror-symmetry: They mirror across their north-south- and east-west-axis as well as along their northwest-southeast- and southwest-northeast-diagonals.
When playing you quickly realize that these challenges tend to be much harder to solve but also much more pleasing. The way in which the asymmetric individual pieces combine to together make the symmetric whole is non-obvious, very satisfying and symbolic as well.
Gerald claimed to have created a lot of these, shared some, and planned to eventually share them all. Most unfortunately he died before he had the chance to do that.
Chapter #2 – The Solver
An occupational hazard faced by many software developers is the urge to throw code at all problems they encounter. Especially at those designed to be recreational puzzles. I believe it is the allure of clear requirements and no deadlines or other commercial pressures that keeps the fun in building these systems as opposed to doing development for profit where a muddle of externalities frequently gets in the way of clean design.
When faced with Fridge IQ I naturally succumbed to the same temptation. So I built a solver. The algorithm is simple recursive-descent with backtracking.
In plain text it can can be summed up like this:
- Given the outline of a challenge and a set of pieces.
- Select any single pieces from the set available. You may try to do that in a clever way to minimize the total work to be done.
- Make a list of all the locations the piece can go inside the challenge.
- (The backtracking part) If that list is empty, there is no solution. Take one step back, remove the piece you placed last and try that in the next position from its candidate list.
- If your list is not empty, place the piece at the first of the locations from it.
- (The recursive part) Start the same process with the current position and the remaining set of pieces.
- When there are no pieces left this means they all have been placed. A solution has been found. Celebrate!
I wrote the code in Python and played with various interesting bits in doing so.
To do the geometry I integrated Shapely. Shapely integrates function from GEOS and thus can trace its roots back to geographic information systems. In the context of the FridgeIQ-solver it turns out to yield useful primitives for describing polygons and their spatial relationship. It can be used for things like checking for overlap or creating unions of shapes.
A representative line for what Shapely brings to the table could be this:
return outer.difference(inner).union(octagon.difference(inner_square))
Given polygons named outer, inner, octagon and inner_square it produces a complex polygon with five holes to make this challenge:

And a possible solution for it can also be represented as a layout of polygons like this:
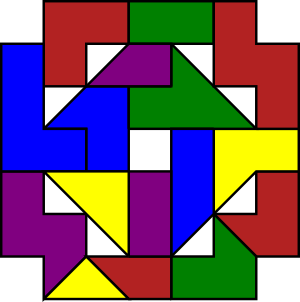
Chapter #3 – Completism Strikes
Faced with Geralds beautiful challenges one terribly obvious question to ask yourself is: Are these all that exist? How can we find out?
This turns out to be a much harder problem than solving a given challenge.
First we need to add an extra constraint. If all we ask for are the four symmetries we end up with infinitely many solutions because there are arrangements consisting of four discrete areas that can subsequently be moved along the major axes. These do not add anything of interest, however, so we will ignore them in the final result.
With that extra constraint it is obvious that there are finitely many challenges so we stand a theoretical chance of listing them all. It is also clear that we only need to consider placing parts on a finite board instead of an infinite plane, although the maximum size of that board is not obvious.
After some thinking I decided to invoke the nuclear option and use a SAT-solver. See the next chapter on how this can be applied to the problem at hand. This choice was mainly driven out of interest in the technology.
After very shallow research I picked Z3 as implementation for the solver, mainly because it was the easiest to integrate and had nice examples that immediately worked.
Chapter #4 – Chasing SATisfaction
In order to apply Z3 the problem needs to be turned into a boolean satisfiability problem. That means creating a set of formulae of yes/no or true/false variables. A solution then is a set of values for these variables that make alle the formulae true at the same time. In SAT-speak such a set is a satisfying interpretation of the problem.
For FridgeIQ I picked the placements of the pieces as input variables. Each piece – when taking on its own – can be placed onto the board in a number of positions and rotations. Each of these is represented by a boolean value which is true if the piece is in that particular position and false if it isn't.
These variables are named in a consistent way. The name is built from the piece identifier (the letter printed on the piece), the grid-coordinates of the placement, and the rotation (0, 90, 180, 270).
Note that this is not a tiling. We want each piece in each legal position on an empty board regardless of any other parts. These positions absolutely will overlap.
So the first job the program has to do is find all possible placements and create these variables. One obvious optimization is that some pieces have inherent symmetry and thus do not need all four distinct rotations.
At this point any set of true and false values for these variables constitute a valid solution for boolean satisfiability. Now we need constraints that shape that into only those combinations that produce a symmetric challenge according to the rules we set out.
The first constraint is that all pieces have to be used and each piece can only be used once. This means that out of the n placement-variable for each piece exactly one must be true and all the others false. Z3 has a specific type of constraint for that. Using the Python bindings this becomes the following one-liner:
z3.PbEq([(x,1) for x in list(map(lambda placement: placement.x, part.placements))], 1)
The next constraint is that the pieces may not overlap. To describe this I thought about the common building blocks of the pieces. Although they can effectively only be placed on a grid they are not made of full grid squares but triangular halves.
As pieces can be placed in any rotation I have elected to model the board as tiled with triangles. Each grid square is split into four right triangles meeting in the center, I call these shards and name them by their compass direction. So each grid square has a northern, eastern, southern and western shard.
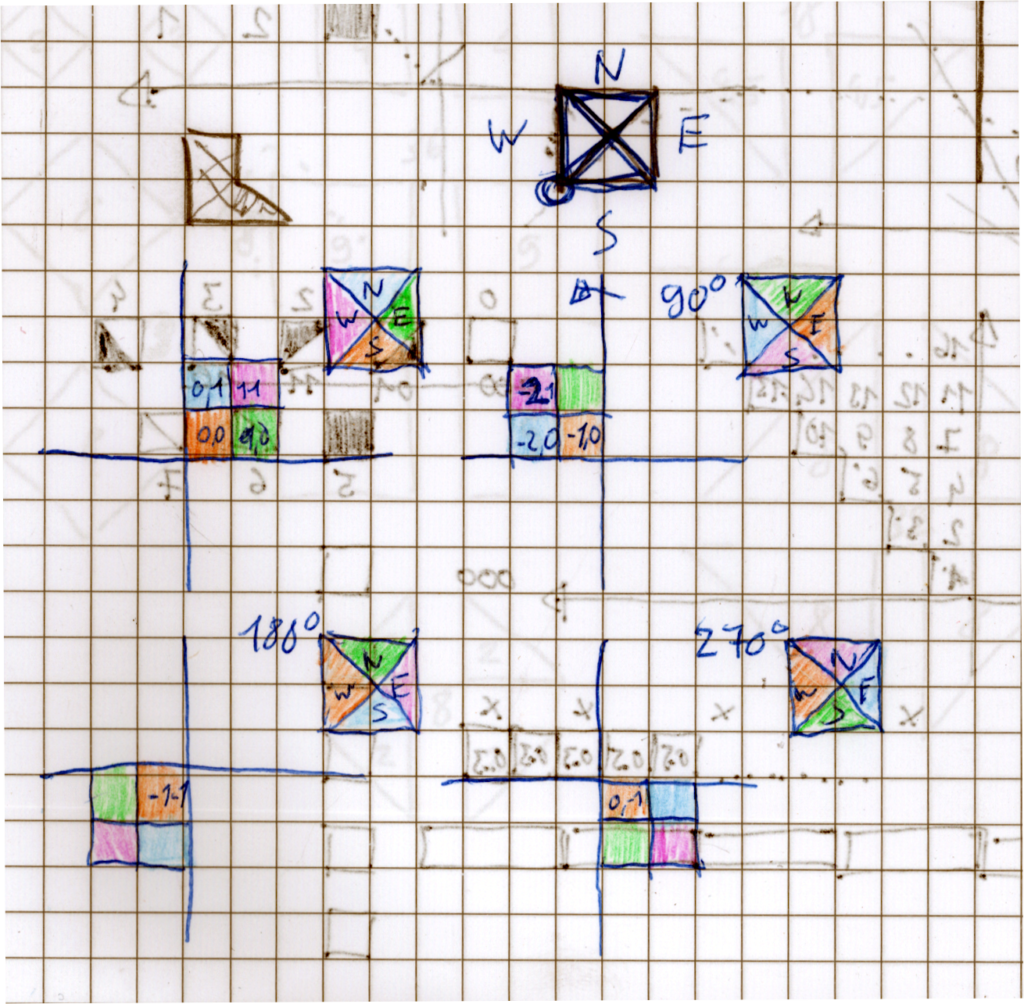
It is easy to calculate which shards are covered by a tile in a certain position. The non-overlaying constraint then follows as: Each shard may be covered by at most one piece. So 0-or-1-out-of-n. In Z3 Python bindings:
for shard in shards.values():
constraints.append( z3.PbLe([(x,1) for x in list(map(lambda placement: placement.x, shard.placements))], 1) )
The symmetry-shards are expressed in a similar way. For each shard on the board there are seven other shards thast form a group and they either all need to be covered or none of them.
After this all that is left to do is to tell Z3 that we want to find a set of placements that satisfies all of the constraints. If there is such a thing.
The program then takes that set, paints it as a nice SVG of the challenge and the solution and saves it.
Finally more constraints are added to exclude this exact arrangement and Z3 is asked again. Now it has to come up with a different answer. We repeat this until there is no more satisfying solution left.
Assuming the constraints are formulated correctly, Z3 works correctly and the underlying hardware works correctly, we now have the complete answer.
Chapter #5: O Of What?
Obviously this is quite a chore. I was lazy, just typed it all out and let it rip. The machine of choice is a Lenovo Thinkpad W530 with an i7 CPU of some sort.
The first solution dropped out after a few minutes, soon followed by more. Exitement ensued. After a few hours the pace slowed as the blocking clauses (arrangements to disregard) mounted. Tens and hundreds of thousands of these accumulated.
After about 10 months of near-constant computation the machine gave an UNSAT-verdict, indicating it had exhausted all the possibilities.
Chapter #6: Show Me The Results
All in all I claim there are 74 "interestingly different" solutions.
After solving the catalog held 79 candidates but there are arrangements that break up into four distinct blocks and those can "wander off" into space and appear at different distances which adds nothing of interest.
So I am dropping these from the count.
Once I was done I was able to compare my result with Geralds list. He has found all of them without using a computer! And more, see the Addendum below for a discussion of what I missed.
Chapter #n+1: What next?
The code for all of this is available on Github. It is not intended for public consumption but for inspiration. Have fun with it, but don't blame me for any trauma or damage it causes.
I have created a booklet from the data in PDF format, had it printed and spiral bound. When printed this way the challenges are printed in 1:1 scale and you can try to solve them on a Fridge or the paper directly. I have also included solutions for all the challenges. The booklet is available for download here.
Gerald claimed to have a lot more challenges than the ones I have recreated through brute force. One of them I have proven (for a very soft usage of the word) using my solver to be impossible if you stick to the rules of FridgeIQ. If, however, you allow flipping of the chiral pieces, it can be done.
Once Gerald convinced himself that he had found all the snowflake-challenges he started flipping pieces to find even more.
That fact and a little playing around indicates there is more to do…
Addendum: Mixed-parity
As expected I have found a serious oversight in my code which became obvious when comparing my results to Geralds notes.
Challenges according to the rules come in two basic flavors: Those centered on grid-lines and those centered on grid-cells. I have named these even and odd symmetry in my implementation and I have discovered all evenly- and oddly-symmetric challenges.
Gerald, however, was more general than that and has created challenges consisting of two distinct parts. A ring and a center. And rings and centers can have mixed parity! All of his challenges that are missing from my list are of that kind.
I have updated my code and in another round it has identified all of Geralds extended versions and found no more.
TODO: Update the booklet to include the new challenges.
Addendum: 3D printer
I have created CAD-Designs for a more solid FridgeIQ set that can be produced on a 3D-printer. In the back there are recesses for simple round magnets to press-fit or super-glue in:

These are available for download on Thingiverse.